Channel capacity of humans as information processors

One way to examine the limits of human information processing is to ask how much information can a person can reproduce from some stimulus they observe. In this framing, we can model the observer as a communications channel using tools from information theory. This figure (Pollack, 1953, p. 422) depicts the model: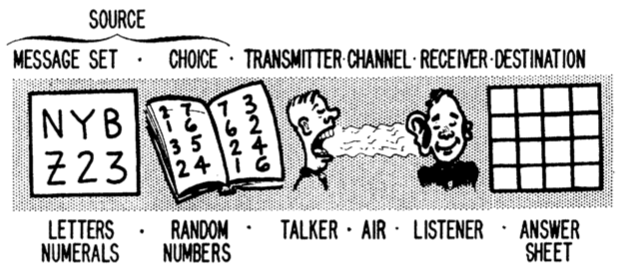

A perfect communications channel could reproduce any input you gave it. In practice, most channels (including humans) produce more errors as inputs contain more information. The behavior is usually asymptotic: a channel transmits its input perfectly until some threshold. Past that threshold, which we call the {channel capacity}, the correlation between outputs and inputs falls, and the total number of bits of transmitted information remains constant.

Experiments on human Span of absolute judgment can be used to model humans in this way. Miller’s review (1956) of the empirical data suggested that human channel capacity for unidimensional stimuli is about {2.6} bits.

For example, here’s a figure from Miller (1956, p. 83), using experimental data from Pollack (1952, 1953) on human absolute judgment of pitches, reframed with an information-theoretic approach.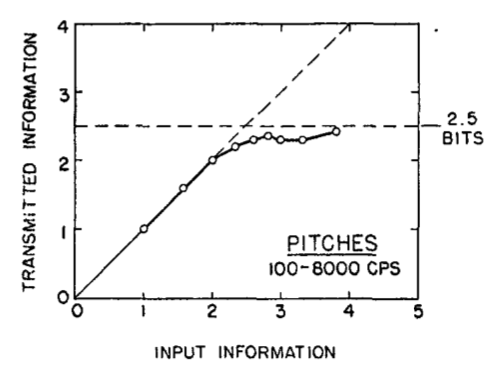

Q. If you know a subject’s span of absolute judgment (for single-item, unidimensional magnitudes), how would you find their channel capacity?
A. channel capacity = log_2(span of absolute judgment)

Q. Why is the span of absolute judgment related to human channel capacity by a log2 relation?
A. Channel capacity is expressed in bits. If the span of absolute judgment is 8 categories, you need log2(8) bits to represent every state.

References

Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two

Pollack, I. (1952). The Information of Elementary Auditory Displays. The Journal of the Acoustical Society of America, 24(6), 745–749. https://doi.org/10.1121/1.1906969

Pollack, I. (1953). Assimilation of Sequentially Encoded Information. The American Journal of Psychology, 66(3), 421–435. JSTOR. https://doi.org/10.2307/1418237