Ebbinghaus, H. (1913). Memory: A Contribution to Experimental Psychology (H. A. Ruger & C. E. Bussenius, Trans.). (Original work published 1885)

This seminal book on memory was one of the first rigorous empirically-minded works of experimental psychology. The experiments follow from a bold central idea: perhaps the dynamics of memory behave something like a physical law, like gravity or electricity. For instance, he observes that re-learning something after it’s been forgotten once is much easier. He suggests that this might not be an ineffable phenomenon of the soul, but something like a physical process, like wearing a needle into a record. And if that’s so, perhaps we can characterize those dynamics—at least to some extent—in that way that we’ve characterized other physical laws.

Ebbinghaus understands that memory will probably behave differently in different situations, and for different people. But if you somehow hold those differences constant, are there consistent relationships guiding the dynamics of memory? How does forgetfulness vary in response to time, recollection, and content?

A key intuition: visual perception is certainly variable and depends on our expectations and memories… but it’s at least somewhat constant: “we are on the whole sufficiently able to see a house just when we want to see it and to receive practically the same picture of it ten times in succession in case no objective change has occurred.” Ebbinghaus carefully constructs experiments which try to hold as many factors constant as possible.

His experiments also contend with our inability to directly access our mental states, except at extremes. One key insight for him is the observation that re-learning something after it’s been forgotten once is much easier.

He’s trying to systematize memory, to understand its dynamics analytically. He wonders: if I measure the schedule of repetitions to learn something “by heart,” will that same schedule always work? Can you define with certainty the point at which something has been learned to that level? This is the motivation for the nonsense words and many other experimental properties: he’s trying to control for natural variation in the environment.

I’m not actually convinced that the attempts to hold everything constant are the best approach. Given that it really is quite difficult to hold everything constant, aren’t RCTs the way forward? The first psychology RCTs were apparently in 1885 in the US, and Ebbinghaus may not have known about them.

Ebbinghaus speaks to my frustration with using frequentist probabilities to express retention: the effects in question arise from many highly varying causes in combination. We’d like to understand those causes, but we can’t, so we make do with these unfortunate statistics, so long as they “run through small circles of numerical values symmetrical around a middle value.” He ends up using conformity to normal distributions (still a novelty at the time!) to validate his measurements.

E. found that sometimes if he could fluently recall a sequence one time, he would be unable to repeat it again immediately thereafter. Some environmental factor was at play.

Chapter 4: normality of distributions

E’s first question is: are the times required to measure various series consistent enough that their averages could be interpreted as obeying some kind of physical law (i.e. are they normally distributed?)

I’m having difficulty picturing what E actually did. Did he read the sequences repeatedly, over and over again, until he could remember them? I think that’s what he’s saying—and what he’s measuring is how long it took to complete this process, i.e. which is a proxy for how many repetitions it took.

Quite a grueling test: 84 samples in the second series, with an average time of 20 minutes.

Anyway: E finds that the total time required to learn the sequences of nonsense-syllables was normally distributed, implying that there may be some underlying law characterizing memory.

He sets up his analysis to compensate for an effect he suspects will occur: that over the course of a memorization series, he will become fatigued. But in fact, he doesn’t observe this. Instead, he observes an oscillation of time taken over the course of the series; he suggests there might be some “periodical oscillation of mental receptivity” according to the ebb and flow of fatigue.

Chapter 5: Learning cost vs. number of syllables

This chapter begins with the observation that longer sequences require more time, effort, and repetition to memorize.

He rapidly makes a key observation from his experiences: he can usually remember seven syllable sequences after only one reading, and occasionally eight. Six syllables are almost always doable. From this he makes a critical suggestion: “a single attentive reading involves an unnecessarily large expenditure of energy for an immediately following reproduction.” i.e.: there’s wasted motion!

He finds that indeed, the number of repetitions necessary increases rapidly with the number of syllables. 12 syllables need 16 repetitions; 24 need 44. An incredible conclusion: 7 syllables can be memorized in one reading—i.e. 3 seconds—but 35 syllables require more than 50 repetitions: concentrated effort for 15 minutes!

A second series of samples from his experiments were collected in a way which allowed comparison, which E was able to use to verify that the curve of repetitions vs. number of syllables was fairly consistent for him.

He also memorized stanzas from Don Juan and found that prose required many fewer repetitions to be successfully memorized: perhaps as little as 1/10 the amount which would have been required for nonsense syllables.

Chapter 6: stability of memory vs. number of repetitions

Another key intuitive insight: even when repetitions don’t result in flawless reproductions, they clearly pave the way for subsequent errorless recall. E suggests the metaphor of “the series as being more or less deeply engraved in some mental substratum,” with that depth varying by the number of repetitions. So: what’s the nature of that relationship? Is it linear? Inverse-squared? etc…

He defines the “inner stability” of a series as the “amount of work saved in the relearning of any series as compared with the work necessary for memorizing a similar but entirely new series,” across a period of 24 hours. He wonders: is this a general measure? That is, can changes be made in the controllable conditions (e.g. the interval, sequence sizes) through proportional scaling? (The answer will be “sort of.”)

He conducts an experiment to explore this by varying the number of repetitions in the initial sequence (varying from 8 to 64) and observing the effects on the subsequent time costs to learn the series.

He observes a roughly linear decline in the latter as the former increases. But he’s also interested in the time savings in the second session from the repetitions of the first. Given the linear decrease, he finds what’s basically a constant time savings of ~2 seconds per sequence’s first-session repetition (each of which take ~7 seconds).

One interesting thing about these results is that E knows from prior experiment that around 31 repetitions are necessary for faultless immediate reproduction. But in the current experiment, he does trials in which he continues repeating up to 64 repetitions, and those tests produce correspondingly lower re-memorization costs in the second session. This is strong evidence for the notion that memorization isn’t a binary effect but rather a continuous phenomenon: extra effort didn’t produce any observable effects in the first session, but it did produce observable effects in the second session.

E notes that the linear relationship found here does seem to taper off as the number of repetitions increases. Experimenting with shorter sequences, he wasn’t ever able to make himself able to recall the sequence on the first repetition 24 hours later.

Chapter 7: forgetting vs. time

E explores: what’s the time savings in re-learning these sequences vs. the interval between initial learning and re-learning? This should correspond to the amount of forgetting. He finds a beautiful inverse exponential—which he doesn’t plot! So I’ll do it for him.

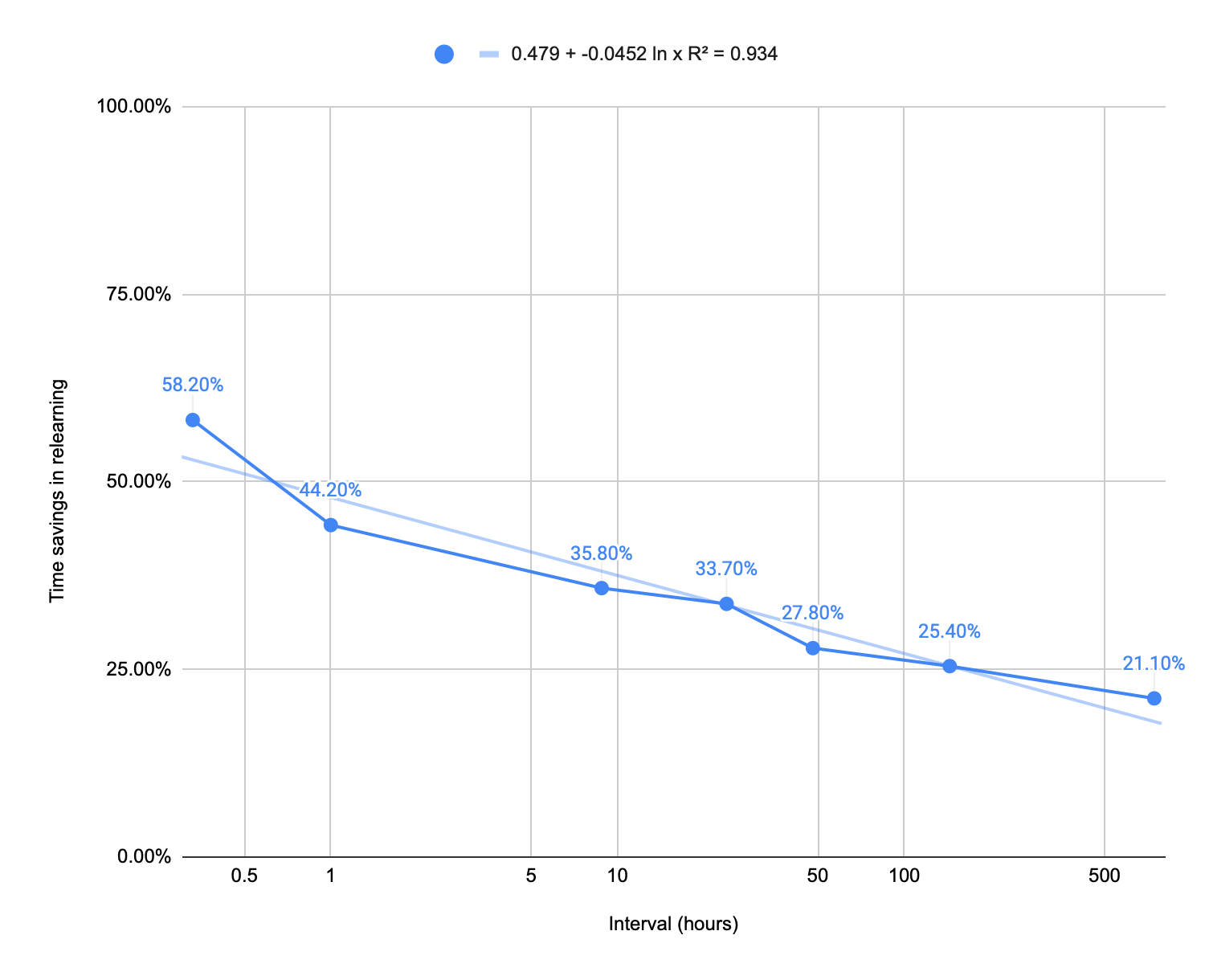
Quite lovely.

Chapter 8: retention vs. repeated learning

E says it’s “sufficiently well known” that something learned twice fades more slowly than something which fades once. No citation. Common knowledge? Intuition?

His experiment doesn’t actually establish spaced repetition. Instead, it simply establishes the impact which 1-day-interval repetition has on memory. His approach again relies on sequences which are too difficult to fully memorize: he’s observing the decline in time required to re-learn the sequence in subsequent trials.

He observes that longer sequences have a greater re-learning savings in the first repetition, perhaps because “that which is learned with difficulty is better retained.” He finds that subsequent repetitions offer accumulating savings on re-learning, initially in proportion to item complexity (1-2 and 2-3) but later roughly even. The curves in re-learning savings looks roughly like an inverse power law for three of the four series.

He closes the chapter with a critical observation about spaced-vs-masse practice. In chapter 6, he found that a 12-syllable series learned with 68 repetitions needed 7 repetitions the following day to re-learn. But in this experiment, he found that 38 repetitions spaced out over three days produced the same result on the fourth day: 7 repetitions to re-learn. That’s a very exciting result, and it suggests that large differences in effort may be required with different schedules (i.e. the Spacing effect).

Chapter 9: sequence association

In this chapter Ebbinghaus conducts a sequence of experiments organized around how we store associations between stimuli in memory. One theory is that there’s a simple pairwise association, but Johann Herbart suggests that the relationship between pairs of stimuli in sequences is continuous in strength, decaying with distance.

E demonstrates that this is indeed the case through another re-learning experiment, this time re-learning modified variations of the original sequence created by taking every Nth element. He found that the re-learning savings vary inversely with N—i.e. the separation between the original elements of the sequence. But a variation created by randomly shuffling the elements yielded no time savings. So something about the sequence is indeed being memorized.

In another experiment, he re-learned reverse sequences (and reverse-every-second-element) and found that learning the forward sequence did indeed confer some re-learning savings to the reverse sequence and its variations, though to a smaller degree.

He also finds that the distant-associate memories are strengthened with more repetitions, as in chapter 4.

His final experiment uncovers a fascinating result: indirect strengthening of associated sequence elements. Skipping the fine details, he finds that re-learning the derived sequence X1, X3, X5, … makes it faster to subsequently re-learning the derived sequence X2, X4, X6, …. This suggests that retrieval practice also strengthens strongly associated memories.

A nice quote (the first RCT in psychology was conducted the same year this book was published, but in the US, and E probably didn’t know about it):

And because of the modest requirements which in psychology are so often imposed upon explanations, this view will doubtless for a long time serve to make dim the vision and so prevent the frank recognition of this as one of the most wonderful of all riddles, and it will also act as a hindrance in the search for its true understanding.And because of the modest requirements which in psychology are so often imposed upon explanations, this view will doubtless for a long time serve to make dim the vision and so prevent the frank recognition of this as one of the most wonderful of all riddles, and it will also act as a hindrance in the search for its true understanding.