2023-03-31 Patreon letter - Memory systems and problem-solving practice

Private copy; not to be shared publicly; part of Patron letters on memory system experiments

One problem with most discussion around memory systems is: the real goal isn’t to remember answers on flashcards; it’s to expand your capacity to think and act in the world. Sure, your app says you can remember this set of cards for months. But what does that mean in terms of what you can do, thoughts you can think? The connection is far from clear. If our goal is to produce real-world capacity, rather than rote recall, how should memory systems be used, designed, redefined? I’ve wanted to dig into these questions for years, but I’ve found it quite tough to establish an effective experimental context. Happily, this month, I’ve been able to watch closely as a student struggles to transfer knowledge from his memory system practice to complex problem solving.

I’ve been acting as a “personal learning assistant” for “Alex”, an adult learner studying physics in service of a meaningful project. We talk every day or two about problems and progress in his learning journey; I listen in on his tutoring sessions; I coach him on handling challenges which arise; and I prototype interventions which might help. This month, Alex has been studying electrostatics from a classic textbook by Young and Freedman. I’ve written memory prompts to reinforce the content—about 70 for each chapter we’ve worked through, covering the material on declarative, procedural, and conceptual levels.

Now here’s the trouble. After Alex read each chapter and completed a few rounds of memory practice, he still found the book’s exercises very difficult. I’m sure the memory practice helped: he’s able to recall long equations and definitions from memory when solving problems. Yet detailed memory practice wasn’t enough, on its own, to let him solve complex practice problems independently. He got stuck and made significant errors.

Then, after many hours of problem-solving, Alex found that the answers came more easily. Something important happened when solving those exercises, above and beyond what occurred when he read the textbook and did detailed memory practice. It certainly wasn’t cheap: I’d guess he spent at least four times as long solving problems as he did reading and reviewing the text.

On some level, this isn’t surprising. Sure, of course, you can’t just read about a topic. You can’t even just answer lots of questions about a topic. You have to do a topic. Fine. But what’s happening, cognitively, during that problem set? Can we cause those changes more effectively or efficiently, e.g. through some kind of targeted practice? What are the implications for topics which don’t come ready-made with problem sets? And: how can we ensure that whatever insights are acquired during this period are retained, like the other material reinforced through memory practice?

Transfer-appropriate processing

For one set of answers, we can look to a theory called “transfer-appropriate processing”, which suggests that our ability to remember information depends in part on how well the processing involved in encoding matches what's involved in retrieval. It's not necessarily enough to just practice recalling some information: practice should require processing that information in the same way you expect to be processing it when you want to use it later.

I saw something like this firsthand with Alex. He could fluidly explain to me how electric fields relate to electric forces, but he struggled to apply that knowledge in a problem where he needed to find the force that a given field would exert on a given charge. Once I demonstrated how he could do that, he quickly saw the connection to the conceptual explanation he’d just given. But that connection was a separate thing from the explanation itself—not one and the same as the explanation.

Cognitive psychologist Garrett O’Day recently ran a relevant series of experiments. He aimed to explore the impact of transfer-appropriate processing on retrieval practice, in the context of complex problem-solving. In one experiment, he gave undergraduates a brief tutorial on Poisson processes. The “practice” group was tested on recalling the procedural steps to solving a kind of Poisson process problem. The “control” group spent the same amount of time reading more worked examples. Then they were both asked to solve problems like the ones they’d been studying. This is the sort of situation which would normally produce a “testing effect”—active retrieval usually produces better performance than passive re-reading. But it didn’t. The groups performed about the same—poorly. O’Day ran a follow-up experiment in which the “practice” group repeatedly solved similar practice problems with feedback, rather than just recalling the procedural steps. This time, on a post-test one week later, the practice group substantially prevailed.

Studying worked examples wasn’t enough; rehearsing the procedural steps wasn’t enough. Both of those groups performed poorly on a post-test. O’Day’s experiments suggest that to become good at solving problems, you need to practice solving problems, ideally with feedback. Theoretically, transfer-appropriate processing suggests that you don’t need to solve problems, per-se; you just need to practice doing something which involves a similar kind of cognitive processing. I’m not immediately sure what that would be. Maybe it would be enough to set up a problem or to take a single “step” in a problem-solving sequence. I’m not yet aware of any experiments along those lines.

Schema acquisition: building problem-solving flexibility

O’Day’s findings highlight another challenge. When test problems were similar to practice problems, practice produced good performance. But when the test problems required small changes to the procedure, performance fell. The gains of practice didn’t transfer.

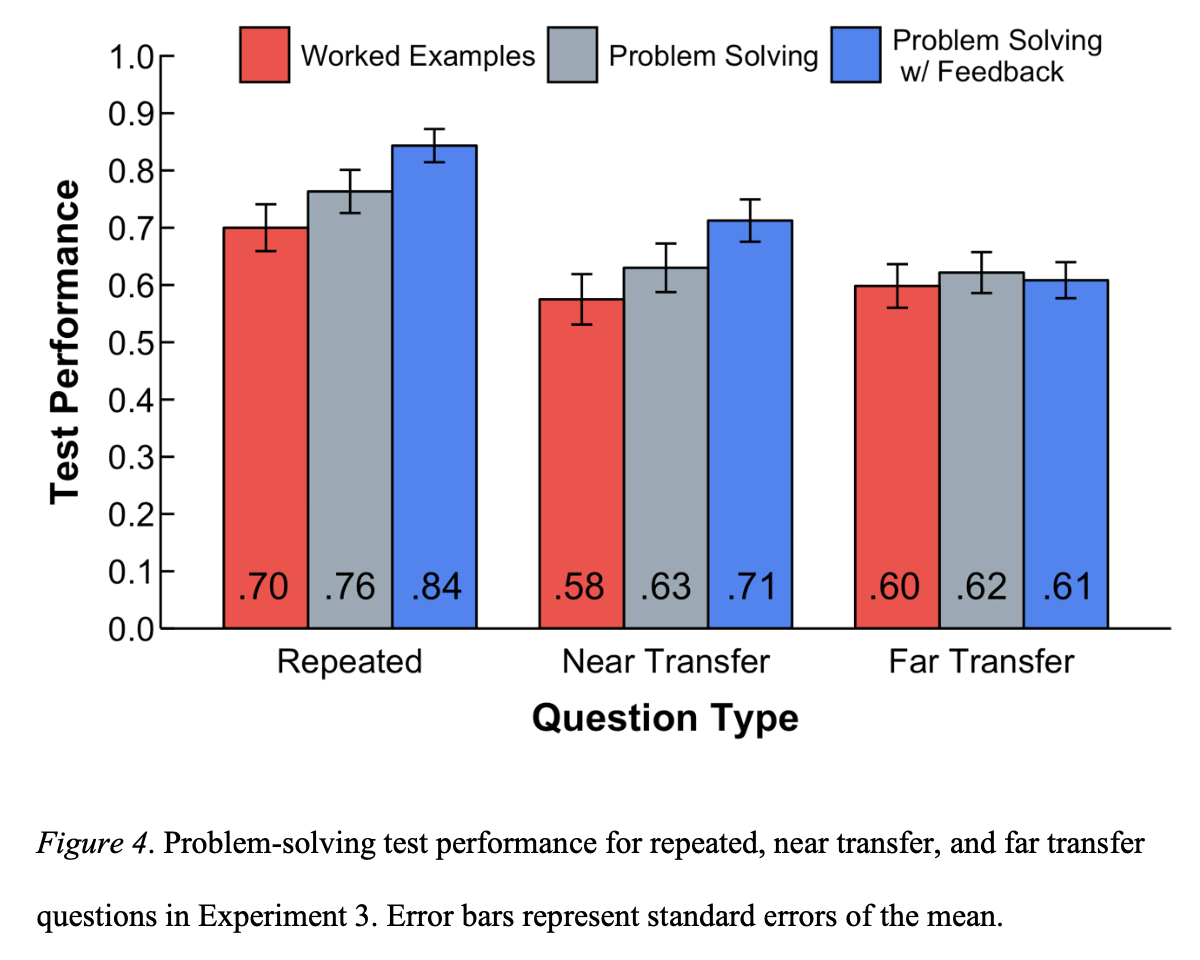
Cognitive psychologists Yeo and Fazio observed a similar result across several experiments using similar materials. But they observed something else of interest: in an experiment where students struggled with the practice problems (< 50% correct), students were better off studying worked examples, rather than solving practice problems. Then, when the materials were changed in later experiments to produce better problem-solving performance during the learning phase, the testing effect returned.

Yeo and Fazio suggest that we’re really observing multiple interacting processes. On the one hand, students need to move what they’re learning into long-term memory and build fluency. Practice and testing support that goal. But to tackle the transfer problems on the test, students also need to generalize what they’re learning. The literature calls this “schema induction”. The claim is that when experts solve problems, they lean heavily on schemas, structures “that permit problem solvers to categorize a problem as one which allows certain moves for solution”. To build flexible problem-solving capacity, you need to acquire these schemas. That’s often done through induction—noticing patterns across a set of problems, noticing that a particular set of moves seems to help.

Another cognitive psychologist, John Sweller, suggests that problem-solving practice poses an important trade-off. Difficult problems may create stronger memory encodings, but they also tax your working memory, creating “cognitive load”. You may end up with little remaining capacity for noticing patterns in problem structure, “acquiring schemas”.

In Yeo and Fazio’s first experiment, the problems were quite difficult, and students were better off studying worked examples than solving practice problems. The authors suggest that’s because students experienced less cognitive load when reading worked examples than when solving problems. And so those readers would have spare capacity for schema acquisition—though the penalty was that they forget what they learned more quickly.

In their second experiment, Yeo and Fazio made the practice problems easier by making the problems’ surface features identical (only the numbers were changed). That helped: students who practiced solving problems were better off than students who studied example problems. But their transfer performance was poor, which makes sense because they practiced a bunch of identical problems. Students built durable memory of what was involved in the problems they practiced, but they didn’t acquire general schemas.

So, in a final experiment, Yeo and Fazio made the practice problems easier, but varied their surface structure. Students’ transfer performance improved enough that it no longer exhibited a statistically significant difference with performance on identical problems. The authors suggest that this experiment’s practice problems were varied enough to generalize over, and the cognitive load was light enough that schema acquisition was possible. Unfortunately, their experiments weren’t really designed to test this particular hypothesis, so we’re left making cross-experiment comparisons for now.

The rough implication here matches common sense. Schema acquisition and memory are at least somewhat independent. You can notice patterns, but fail to remember them durably; you can reinforce your memory of problem-solving, but in a brittle fashion which won’t transfer to unfamiliar problems. Cognitive psychologists often talk of desirable difficulties—productive struggle which induces more complex processing—but students do face a real possibility of undesirable difficulties. If you want both flexibility and durable fluency, then you should practice, but along a gentle slope. You don't want to overload your working memory so much that your mind can’t reorganize its representations of the relevant concepts. And, when you’re getting started, that will often mean that you’re better off carefully studying a worked example, rather than solving a problem yourself. To put it too reductively (because memory is of course involved in building flexibility), you want to be able to solve problems in the first place, and then you want to build fluency so that you can solve them for the long term.

None of the papers I’ve mentioned has anything to say about maintenance—that is, keeping this kind of transferable problem-solving performance durably accessible for a long time. My guess would be that once these flexible schemas are acquired, you could reinforce them through ordinary distributed retrieval practice. As we discussed in the last section, you’d want to actually solve problems, rather than just retrieve the procedure. Maybe you could set up problems with “friendly numbers” so that they could always be readily solved in your head. And to reinforce those flexible schemas, you’d want the problem to vary each time. One could probably use a language model to generate pretty good variations of that kind, but it’s probably not necessary to have a truly bottomless pool: if practice is widely distributed, you could probably get away with practicing a small handful of structural variations, particularly if the numbers were randomly generated.

It’s worth noting that at this point, we’re approaching the territory of intelligent tutoring systems (ITS), another branch of educational technology research. Heavily inspired by the same theory of cognitive load, these systems are laser-focused on finding the smoothest problem-solving slope to any desired destination. They’re usually less concerned with flexibility and durability as goals, but it’s interesting to consider how memory systems might be adapted with ITS techniques, or how ITS might be adapted to support flexibility and durability.

Incomplete absorption

In these past two sections, I’ve begun to address some of what’s happening, cognitively, during problem sets, and how we might make some of that activity more effective. But there’s another simple explanation for some of the struggle I’ve been seeing: Alex hadn’t actually understood parts of what the textbook was saying, and he hadn’t noticed.

Unfortunately, the exercises didn’t clearly reveal those holes. Problems relying on missing pieces just felt confusing and difficult, in a diffuse and undirected way. But in think-aloud video of his memory practice, quite a few questions elicited remarks like “I remember that the answer is X, but I don’t see why,” or “I’m confused that the answer is X.” Just as an example, one question was: “Why does the electric flux through a box containing a proton not change if you double the size of the box on each side?” There are many valid ways to answer that question, but the problem here was that no answer really made sense to Alex.

With this question and the others like it, I wasn’t trying to help Alex generate new understandings or acquire general schemas. These questions are really just intended to be straightforward memory reinforcement. They directly recapitulate some important explanation from the text, with similar wording. If Alex can’t produce an answer, but the solution immediately makes sense once he reads it, then more retrieval practice will probably help. On the other hand, if the answer doesn’t make sense, rote repetition isn’t the right fix. If he doesn’t understand why the answer is what it is, then he doesn’t understand the concept we’re trying to reinforce. There’s not much point in just memorizing the answer.

This is an important distinction to understand, and I fear it’s one that memory system designers consistently ignore: the appropriate intervention for a “wrong” answer will vary enormously with the nature of the prompt. If you’ve forgotten something you’re supposed to memorize, then it’s probably fine to review it again until it sticks. If you never understood the answer in the first place, then you need some very different intervention. And there are other meaningful categories. If it’s a generative task (“hum a melody in pentatonic minor”), and you find it too difficult, you might want to browse some examples, or tone down the difficulty of a task (“hum a final bar for this pentatonic minor melody”). If it’s a problem-solving task, you might want to read a worked solution, then add focused prompts about important patterns or procedural steps. Or, ITS-style, you might want to read an explanation of the misconception which your answer suggests, and then queue up some simpler problems which focus on that confusion.

In Alex’s case, I think the most appropriate next step is to simply reread the relevant passage from the textbook. I don’t think the book’s explanations were too confusing; probably his attention just lapsed during those passages. (I think this happens to everyone, more or less constantly, but we just don’t notice.) I’ve linked each prompt directly to a source location, so re-reading is relatively easy mechanically, but it’s more difficult practically. It feels bad to interrupt the smooth flow of a review session to go read a textbook. Also, Alex prefers to review on his phone, and it’d be pretty awkward to pull up textbook pages on that tiny screen. So it’s probably best to flag these questions and to establish a process to work through that queue during study sessions. If the book’s explanation still feels confusing, then the right next step is probably to discuss it together. Or, for some concepts, it may be better to just set it aside for a while and see if it makes sense later.

In Quantum Country, I think our design helped with this sort of situation. You first review every prompt in the context of reading the book, rather than in the context of a memory review session. So if you notice that you’re confused by some answer, it’s much less disruptive to scroll back up a little and re-read. And because the reviews occur every few minutes of reading, the relevant passage won’t be too far away. Readers we interviewed often remarked that they felt an unusual sort of confidence while reading, since they knew the interleaved reviews would ensure they absorbed everything they were “supposed to”.

Why didn’t we use a design like Quantum Country’s for Alex’s physics review? At first, it was because he was reading a physical copy of the book! He later switched to a digital edition. I’ve implemented a PDF reader with integrated memory prompts, but PDF rendering is obnoxious enough that I haven’t yet managed to integrate the interstitial reviews. Right now, prompts are presented in the margins, like last summer’s prototype:

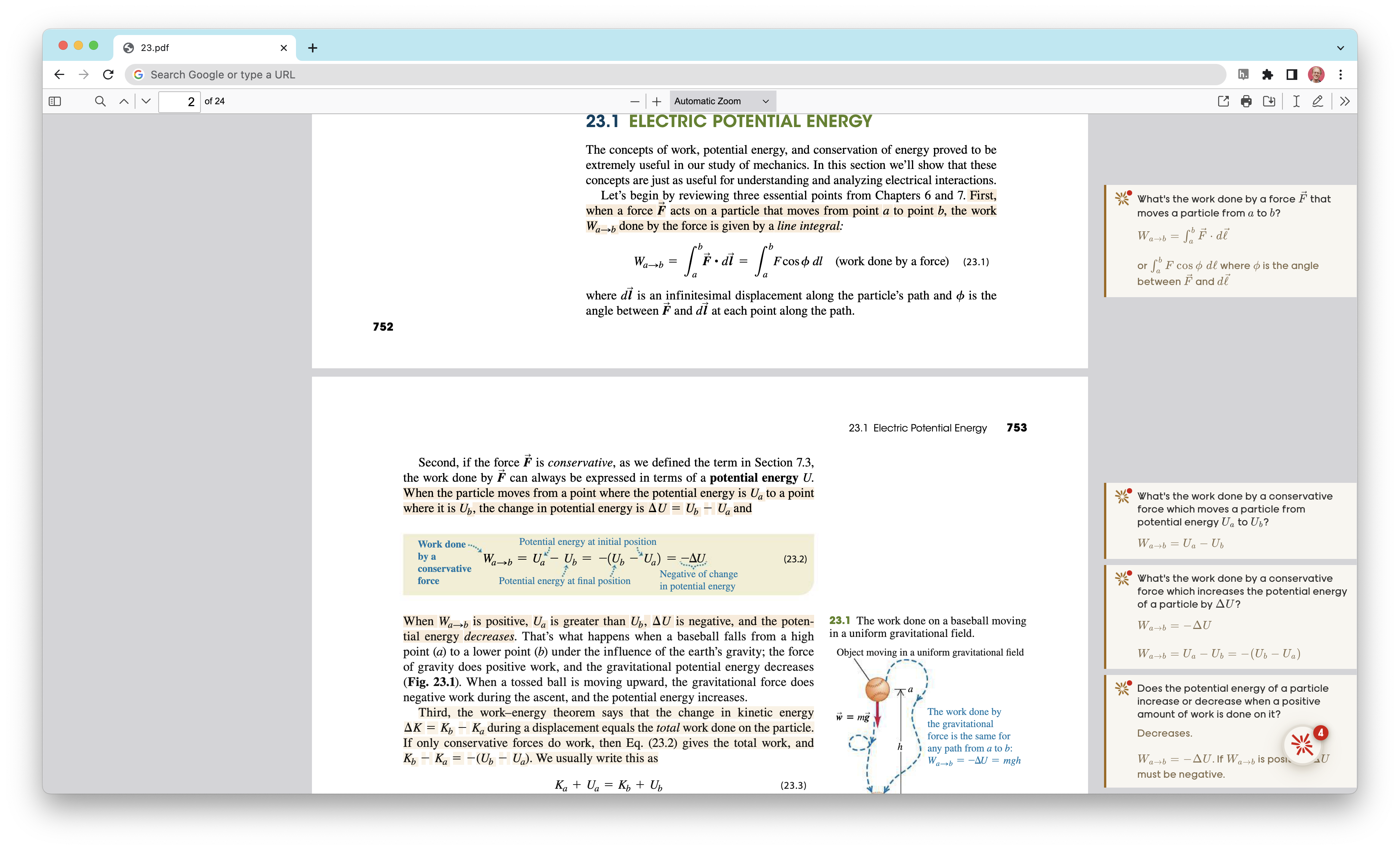
In this discussion, confusing memory prompts play an unusual but important role. Instead of doing the job of reinforcing long-term memory, they act as backstops. They make sure that if you didn’t understand that part of the text, or if you weren’t paying attention, you’ll notice! I think this is quite valuable. The usual alternative is that you try to solve exercises and end up confused or stuck because you’re missing some important conceptual understanding. As I mentioned earlier, the trouble there is that it’s not clear what you’re missing. Even reading a worked solution may not make the missing concept nearly so obvious as the simple prompts we’ve been discussing.

Learning in conversation

In the introduction to his Lectures, Feynman writes:

Problems give a good opportunity to fill out the material of the lectures and make more realistic, more complete, and more settled in the mind the ideas that have been exposed.

I think, however, that there isn’t any solution to this problem of education other than to realize that the best teaching can be done only when there is a direct individual relationship between a student and a good teacher—a situation in which the student discusses the ideas, thinks about the things, and talks about the things. It’s impossible to learn very much by simply sitting in a lecture, or even by simply doing problems that are assigned.

Alex and I have met roughly once a week to discuss the material and to solve problems together. I’m not sure how true Feynman’s claim is, but Alex has told me that these sessions have felt extremely valuable. I don’t think these sessions replace the role of a memory system: we get more out of our time together because we don’t have to review the fundamentals, and he’s not looking things up all the time. And the memory system ensures that much of whatever progress we make will stick.

But I can imagine that in an ideal world, Alex would have me (or a more effective tutor) by his side during 100% of his problem solving time. This isn’t cheating; I’m not making his work easier by giving the answers away. I let him struggle, and when he’s stuck, I ask probing questions which might unblock progress. I can supply raw information where it’s needed. If I notice a misconception, I can ask a question which might create some revealing conversation. I’ll call attention to patterns or connections he might have missed.

It’s hard not to start wondering: could a large language model do some or all of this? I don’t think I’m doing anything terribly special, though I’m certainly drawing on my subject matter experience in both physics and education. A sufficiently good model could also help with the question of how to handle topics which don’t come with ready-made problem sets and discussion questions. There are now six zillion “AI tutor” startups in flight, but none I’ve seen have yet felt like they’re on the right track. I don’t have a clear sense of what my complaint is: too instructional, too interested in “right answers”, not interested enough in discussion and sense-making.

There is one element of our collaborative problem solving sessions which I’d guess these systems would have trouble providing: social energy. Alex is motivated and disciplined, but like all of us, his gumption ebbs and flows. On some days, it can be hard to muster the energy to pick up another chapter. But he’s observed that when we’re working together, it’s much easier to get and stay excited about the learning process. I’ve certainly had that experience when collaborating with others on… well, basically everything!

I’ll close by noting that while I’ve introduced a lot of problems in this essay, I’m thrilled about what I’m learning here. This feels like a basically ideal context for my research. Alex is highly motivated to deeply understand. There are strong pressures on that understanding. He’s struggling, so there’s real opportunity for augmentation. I’m getting an intimate view of his learning process, ample opportunity to intervene, and tight feedback loops on anything I try. It’s exhilarating! Now I just have to deliver.