Human channel capacity increases with stimulus dimensionality

For unidimensional stimuli, the Channel capacity of humans as information processors is only a couple bits, but in everyday life, it seems that we routinely reproduce much more complex stimuli than that. One explanation for this discrepancy is that human channel capacity {increases} with the {dimensionality} of the stimulus.

For example, Miller’s analysis (1956, p. 85-87) of data from Hake and Garner (1951) and Coonan and Klemmer (unpublished communication with Miller) suggest that human channel capacity for points on a line is between {3.2 and 3.9 bits (10-15 categories)}, whereas data from Klemmer and Frick (1953) suggest that human channel capacity for points in a square is about {4.6 bits (~24 categories)}.

Miller’s figure (1956, p. 88) summarizing the data for independently-varying dimensions: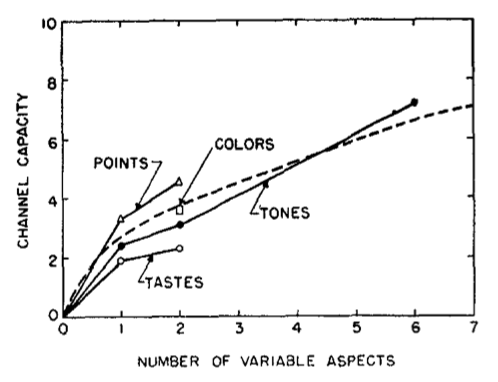

The channel capacity does not increase linearly with the number of dimensions. In fact, as dimensionality increases, channel capacity for any individual variable reliably {decreases} (Miller, 1956, p. 89), so long as {the number of categories to be judged is greater than the dimensionality} (Erikson, 1955, p. 327-329)

This effect appears to persist even when the added dimensions aren’t independent, e.g. when correlating size, brightness, and hue simultaneously to a single variable, the channel capacity was 4.1 bits, versus 2.7 bits for any isolated attribute (Eriksen, 1955, as aggregated by Miller, 1956, p. 88).

Miller conjectures (1956, p. 91) that this effect asymptotes around 10 dimensions, but there was no evidence at that time. Halford et al (1998) review the intervening evidence and suggest that the limit is closer to {4}.

References

Eriksen, C. W., & Hake, H. W. (1955). Absolute judgments as a function of stimulus range and number of stimulus and response categories. Journal of Experimental Psychology, 49(5), 323–332. https://doi.org/10.1037/h0044211

Hake, H. W., & Garner, W. R. (1951). The effect of presenting various numbers of discrete steps on scale reading accuracy. Journal of Experimental Psychology, 42(5), 358–366. https://doi.org/10.1037/h0055485

Halford, G. S., Wilson, W. H., & Phillips, S. (1998). Processing capacity defined by relational complexity: Implications for comparative, developmental, and cognitive psychology. Behavioral and Brain Sciences, 21(6), 803–831. https://doi.org/10.1017/S0140525X98001769

Klemmer, E. T., & Frick, F. C. (1953). Assimilation of information from dot and matrix patterns. Journal of Experimental Psychology, 45(1), 15–19. https://doi.org/10.1037/h0060868

Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. https://doi.org/10.1037/h0043158 Miller - The magical number seven, plus or minus two